递归的介绍

在 vlog.2 的 printf 函数的返回值举例中，我们使用多次递归的方式实现了同一个函数的返回值调用，但这只是一个简易的递归，不算真正意义上的递归，那么什么是递归？

在C语言中，递归就是函数自己调用自己，如果函数的递归没有限制条件，一直无限循环调用下去，代码最终就会陷入死循环，导致栈溢出（Stack overflow）

递归就是递推的意思，递归的思考方式就是将大事化小，将复杂的程序化成简单的代码格式，也就是化成一个个子问题求解，知道子程序不再被分解，递归就结束了

递归的限制条件

值得注意的是，递归也存在限制条件

• 递归存在限制条件，当满足这个限制条件的时候，递归便不再继续
• 每次递归调用之后越来越接近这个限制条件

递归实战应用

求 n 的阶乘

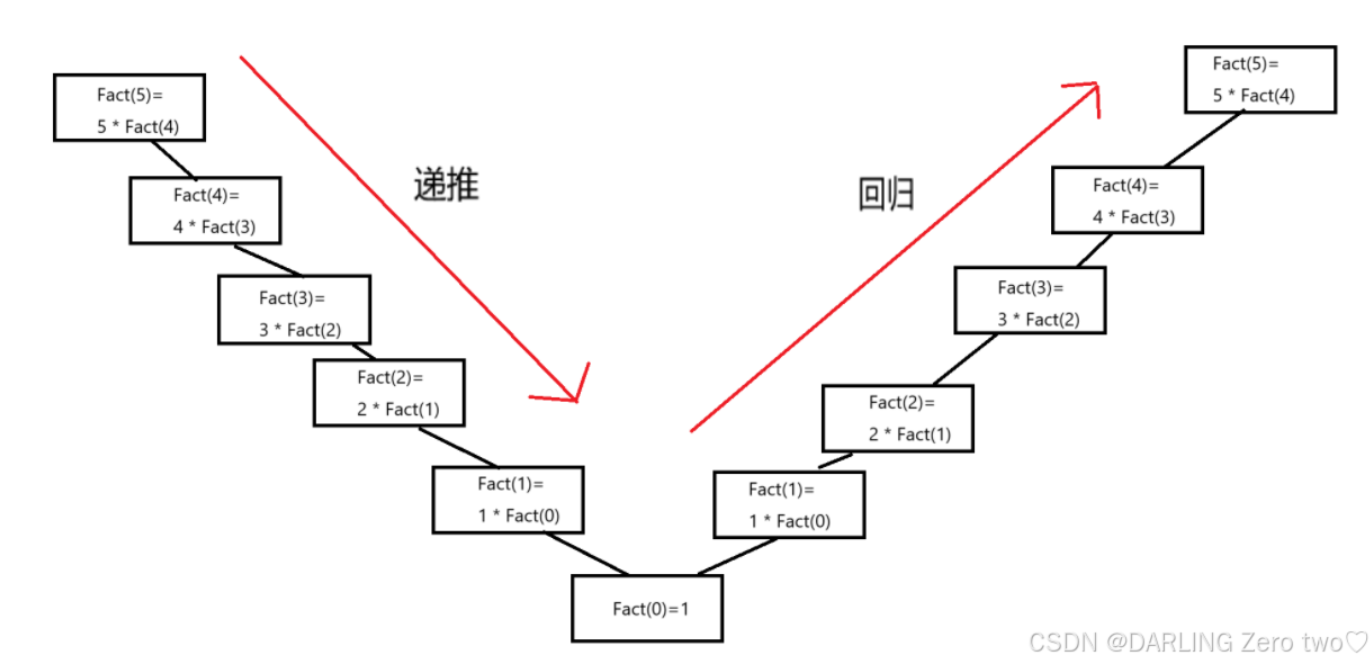
由数学知识可知：n！= n ∗ (n−1)! 当 n == 0 的时候，此时 n 的阶乘是 1 ，n > 0时阶乘可根据公式计算

那么我们可以写出阶乘函数 Fact ，Fact(n) 是求 n 的阶乘，那么Fact(n-1)就是求 n-1 的阶乘
此处不考虑 n 过大导致栈溢出的情况，只考虑合理范围内的 n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
int Fact(int n)
{
if(n==0)
return 1;
else
return n*Fact(n-1);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fact(n);
printf("%d\n", ret);
return 0;
}

该程序的递归思想可以根据画图很容易的理解
在这里插入图片描述

顺序打印一个整数的每一位

输入⼀个整数m，按照顺序打印整数的每⼀位
如果n是⼀位数，n的每⼀位就是n自己
n是超过1位数的话，就得拆分每⼀位
比如：

1234%10就能得到4，然后1234/10得到123，这就相当于去掉了4
然后继续对123%10，就得到了3，再除10去掉3，以此类推
不断的 %10 和 /10 操作，直到1234的每一位都得到
但是这里有个问题就是得到的数字顺序是倒着的

假设我们用函数Print(n)打印n的每一位
那么我们知道1234 % 10 = 4，1234 / 10 = 123

Print(1234)就可以拆分为两步：

  1. Print(1234/10) //打印123的每⼀位
  2. printf(1234%10) //打印4

以此类推,利用递归思想

1
2
3
4
5
   Print(1234)
==>Print(123)                   +printf(4)
==>Print(12)          + printf(3)
==>Print(1) + printf(2)
==>printf(1)

直到被打印的数字变成一位数的时候，就不需要再拆分，递归结束：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void Print(int n)
{
  if(n>9)
  {
     Print(n/10);
  }
  printf("%d ", n%10);
}
int main()
{
    int m = 0;
    scanf("%d", &m);
    Print(m);
    return 0;
}

这里的函数不断地调用，当函数调用完之后依次从最后一个子程序往第一个程序打印

递归与迭代

Fact函数是可以产生正确的结果，但是在递归函数调用的过程中涉及一些运行时的开销

在C语言中每一次函数调用，都需要为本次函数调用在内存的栈区，申请一块内存空间来保存函数调
用期间的各种局部变量的值，这块空间被称为运行时堆栈，或者函数栈帧。
函数不返回，函数对应的栈帧空间就⼀直占用，所以如果函数调用中存在递归调用的话，每⼀次递归
函数调用都会开辟属于自己的栈帧空间，直到函数递归不再继续，开始回归，才逐层释放栈帧空间，
所以如果采用函数递归的方式完成代码，递归层次太深，就会浪费太多的栈帧空间，也可能引起栈溢
出的问题，而且也很耗时间（后期将推出函数栈帧专题）

通常如果使用递归不合适，就可以使用迭代的方式，那什么是迭代呢？
迭代简单来讲就是用循环的方式运行

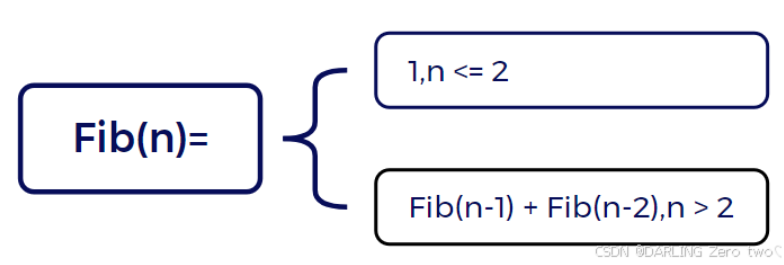
举个例子：求第 n 个斐波那契数
在这里插入图片描述
如果使用的是递归的方法的话，层次会非常深，冗余的计算会非常多

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <stdio.h>
 int count = 0;
 int Fib(int n)
 {
 if(n == 3)
     count++;//统计第3个斐波那契数被计算的次数
 if(n<=2)
     return 1;
 else
     return Fib(n-1)+Fib(n-2);
 }
 int main()
 {
 int n = 0;
 scanf("%d", &n);
 int ret = Fib(n);
 printf("%d\n", ret);
 printf("count = %d\n", count);
 return 0;

根据 count 的次数，在计算第40个斐波那契数的时候，使用递归方式，第3个斐波那契数就被重复计算了39088169次，这些计算是非常冗余的。所以斐波那契数的计算，使用递归是非常不明智的，我们就得想迭代的方式解决

那么迭代的话

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int Fib(int n)
 {
 int a = 1;
 int b = 1;
 int c = 1;
 while(n>2)
 {
 c = a+b;
 a = b;
 b = c;
 n--;
 }
 return c;
 }

不难看出，似乎用迭代的方式去实现这个代码，效率就要高出很多了，但同时我们也不要一直使用，会容易出现程序错误

递归经典问题的拓展

青蛙跳台阶问题
汉诺塔问题

这两个问题将在下一期vlog拓展推出，欢迎大家看我的下一期推文

希望读者们多多三连支持

小编会继续更新

你们的鼓励就是我前进的动力！

在这里插入图片描述