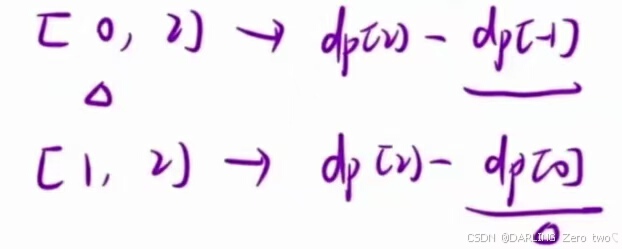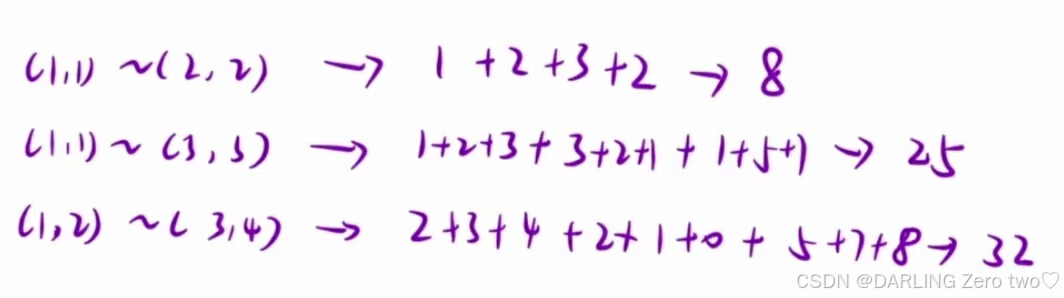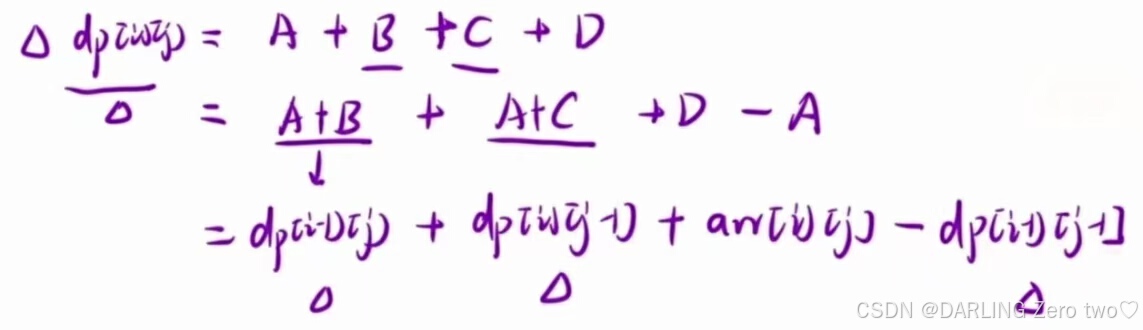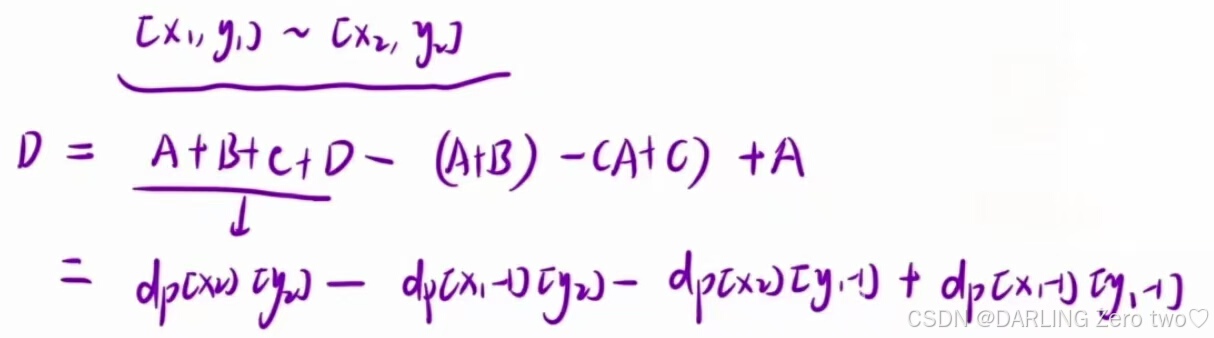概念解析

🚩什么是前缀和算法？
前缀和算法是一种用于高效计算数组区间和的算法。对于一个给定的数组 nums，我们可以预先计算出它的前缀和数组 prefixSum ，其中 prefixSum[i] 表示 nums[0] 到 nums[i] 的元素之和

比如：

数组：
nums [ 1，2，3，4，5，6]
前缀和数组：
prefixSum [1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, 1 + 2 + 3 + 4 + 5]
即[1, 3, 6, 10, 15]

🚩为什么要使用前缀和算法？
假设我们要对数组的一块区间进行检查，元素个数为 n ，检查次数为 q ，那么如果使用传统的暴力解法，即模拟算法，每次检查就要遍历一次数组，那么时间复杂度为 O(n∗q)，即 O(n²)；使用了前缀和算法可以让时间复杂度降级，即O(n) + O(q) ，是一种空间换时间的算法。此时如果 n 和 q 的数据庞大，暴力解法的效率必然是低下的，所以前缀和算法使用是必要的

代码实现

【模版】前缀和（一维）

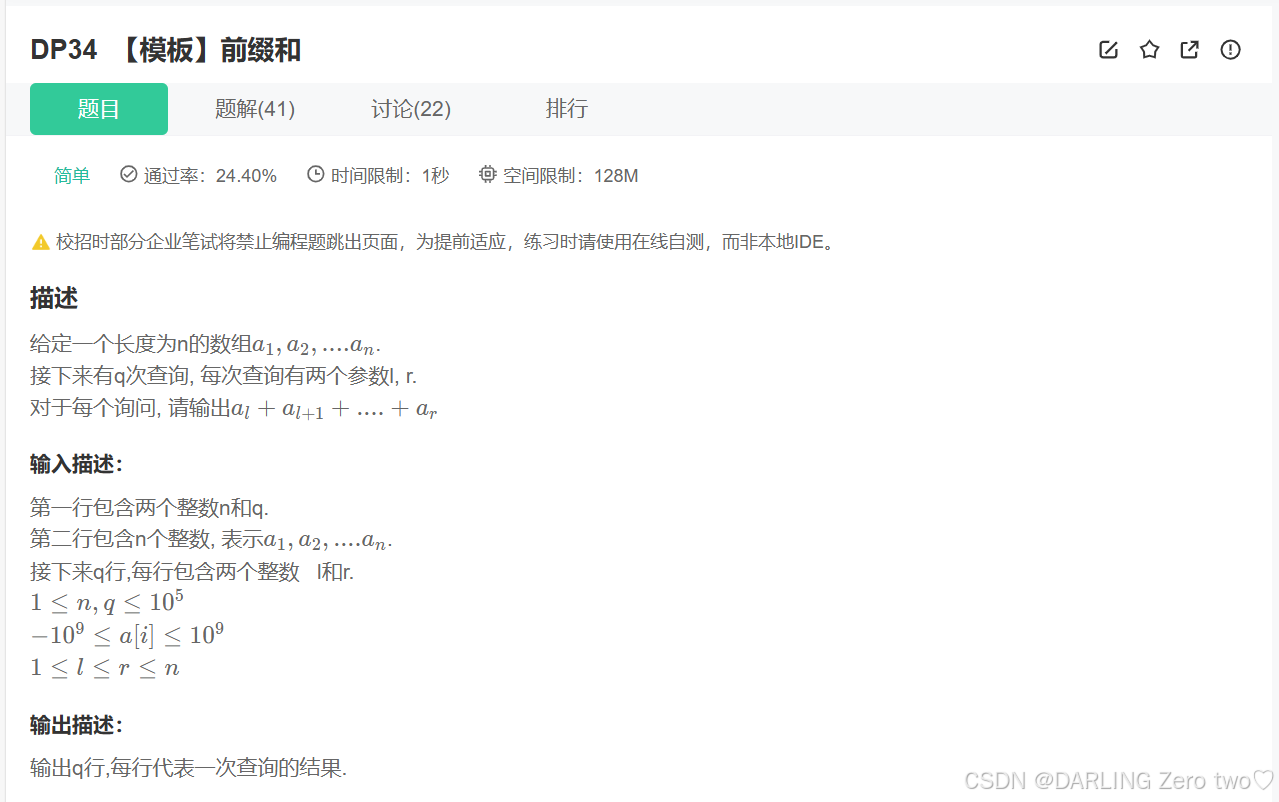
✏️题目描述：

在这里插入图片描述

✏️示例：

在这里插入图片描述

传送门：【模版】前缀和（一维）

原理

💻第一步： 预处理一个前缀和数组

假设有一个数组 arr，dp [i] 表示 [1，i] 区间內所有元素的和，index 表示数组下标（从 1 开始）
请添加图片描述
每一位的元素都可以表示为 dp[i] = dp[i - 1] + arr[i]，即该位元素的和等于前面元素的和加上该位的元素，可能你会无法理解，但本质上是个小的动态规划，会从最开始的元素不断迭代到当前的元素

💻第二步： 使用前缀和数组

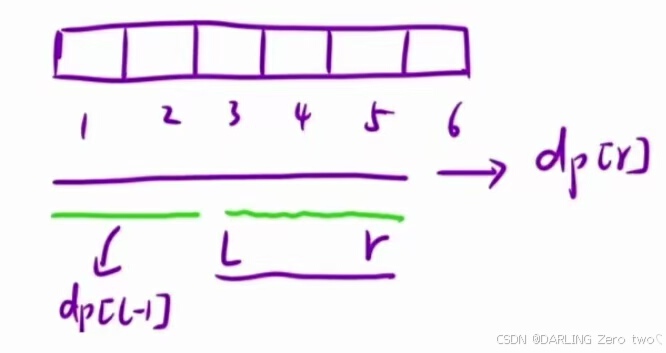
那么回到这道题目，我们要求一段区间内的和

请添加图片描述
假设我们要求区间 [3，5] 的数据和，因为前缀和都是从 1 开始加的，所以我们可以用区间 [1，5] 减去 区间[1，2] 得到想要的区间。取左边界为 L ，右边界为 R，即可总结出公式：某区间的和 = dp[R] - dp[L- 1]

💻细节问题：

为什么 dp 数组从下表为 1 开始？

请添加图片描述
目的是为了添加一个虚拟节点（辅助节点），规避了边界处理的问题。如图所示，如果取区间 [0，2] ，那么左边界 L 取 0 的时候会造成下标为 -1 的情况出现，所以为了避免这种情况，下标从 1 开始存放数据，且下标为 0 处存放数据为 0 就不会影响加和的结果

代码实现

#include <iostream>
#include <vector>
using namespace std;

int main()
{
	//1.读入数据
	int n = 0, q = 0;
	cin >> n >> q;
	vector<int> arr(n + 1, 0);
	for (int i = 1; i <= n; ++i)
	{
		cin >> arr[i];
	}
	//2.预处理出来一个前缀和数组
	vector<long long> dp(n + 1, 0);
	for (int i = 1; i <= n; ++i)
	{
		dp[i] = dp[i - 1] + arr[i];
	}
	//3.使用前缀和数组
	int L = 0, R = 0;
	while (q--)
	{
		cin >> L >> R;
		cout << dp[R] - dp[L - 1] << endl;
	}
	return 0;
}

🔥值得注意的是： dp 数组的容量大小类型应为 long long ，因为存放的数据可能很大，想加后可能会超过 int 的类型大小

【模版】前缀和（二维）

✏️题目描述：

在这里插入图片描述

✏️示例：

在这里插入图片描述

传送门：【模版】前缀和（二维）

原理

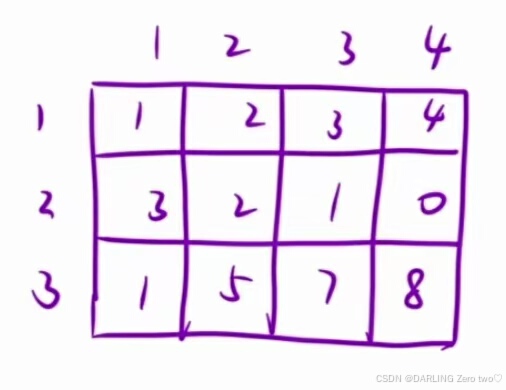
根据示例 1 ，二维矩阵图如下：
请添加图片描述
从一点（x1，y1）到（x2，y2）的表示这个矩阵中所有元素的和

💻第一步： 预处理一个前缀和矩阵

根据题意我们想要求整个矩阵中某个子集矩阵，需要先把求矩阵的模版列出来
所以我们定义 dp[i][j] 表示从 [1，1] 到 [i，j] 位置，这段区间里所有元素的和
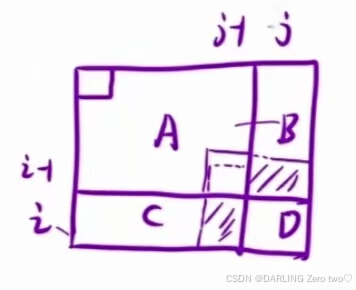
然后把矩阵划分为A、B、C、D四个部分便于求和

请添加图片描述

显然整个矩阵的面积是由四个部分加和而成，但是我们发现B、C的面积不好求得
所以可以进行一些加减的转化

请添加图片描述

主要是一个矩阵要在[1，1] 位置延伸就比较好算，所以通常会结合着 A 计算，多出的 A 要注意减掉，就可以整理出公式：dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1]

💻第二步： 使用前缀和矩阵

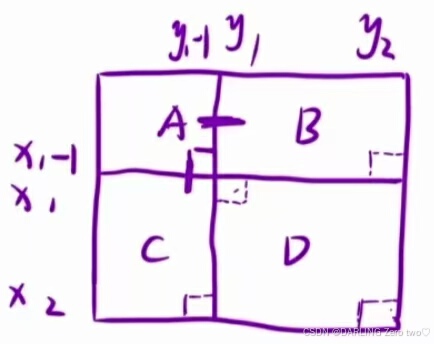
回到题目，我们是要求矩阵中某个子集矩阵，所以根据图形及题意，画出如图：

请添加图片描述

还是和第一步的方法一样，巧用加减法算出矩阵元素和

请添加图片描述
那么可以整理出（x1，y1）到（x2，y2）表示为 dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]，记得要加上多减的一块 A

代码实现

#include <iostream>
#include <vector>
using namespace std;

int main()
{
	//1.读入数据
	int n = 0, m = 0, q = 0;
	cin >> n >> m >> q;
	vector<vector<int>> arr(n + 1, vector<int>(m + 1));
	for (int i = 1; i <= n; ++i)
	{
		for (int j = 1; j <= m; ++j)
		{
			cin >> arr[i][j];
		}
	}
	//2.预处理前缀和矩阵
	vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));
	for (int i = 1; i <= n; ++i)
	{
		for (int j = 1; j <= m; ++j)
		{
			dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];
		}
	}
	//3.使用前缀和矩阵
	int x1 = 0, x2 = 0, y1 = 0, y2 = 0;
	while (q--)
	{
		cin >> x1 >> y1 >> x2 >> y2;
		cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl;
	}
	return 0;
}