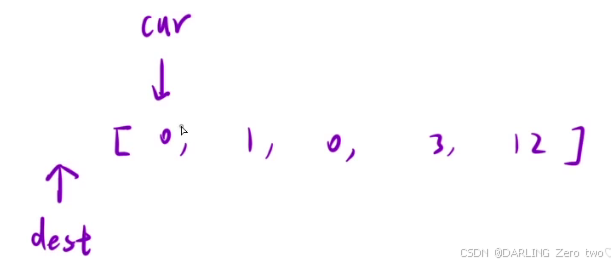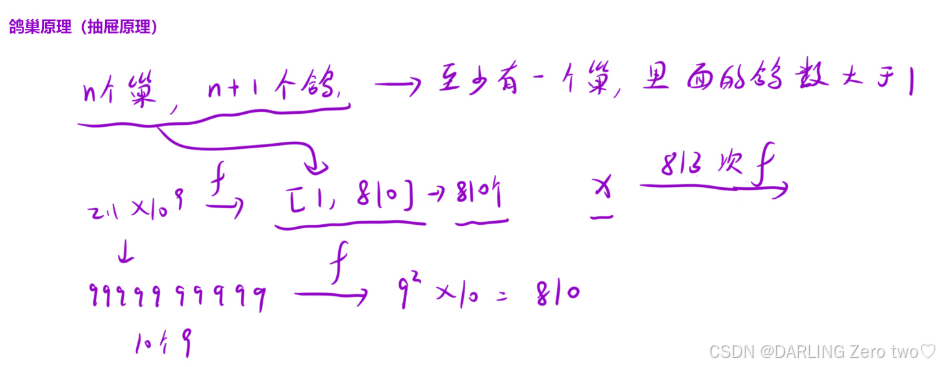概念解析

🚩什么是双指针算法？

在这里插入图片描述

双指针算法使用两个索引来遍历数据结构，可以根据问题的要求，以不同的方式移动，如同向移动、相向移动或快慢不同的速度移动

移动零

✏️题目描述：

在这里插入图片描述

✏️示例：

在这里插入图片描述

传送门：移动零

题解:
💻第一步：

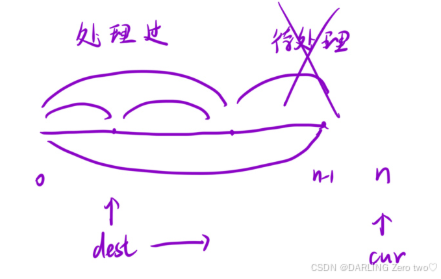
在这里插入图片描述

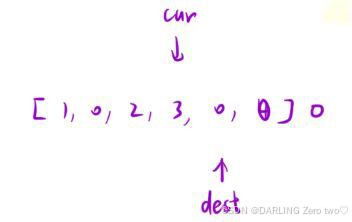
有两个索引 dest 和 cur
• dest 表示在已处理的区间内，非零元素的最后一个位置
• cur 表示从左往右扫描数组遍历数组

在这里插入图片描述

把整个区间划分为三个部分，从前往后分别是非零区间，0区间，待处理区间

💻第二步：

根据题意我们要把 0 都移到数组末尾，所以是要注意是移动，而不是覆盖

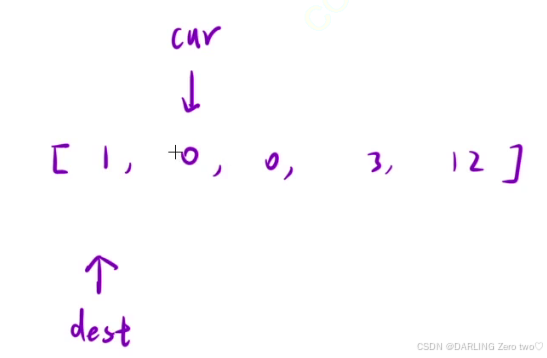
在这里插入图片描述

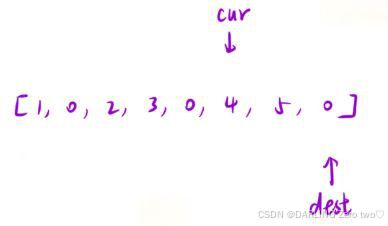
刚开始dest 指向 -1的位置，表示非0区间还不存在，然后 cur 先向右移动，如果为 0 就继续向后；如果为非0，就让 dest 向后一位，然后和 cur 交换（因为 cur 遇到 0 不会改变其位置，所以在 dest 后面必定至少有一个 0 ，通过交换就能一直把 0 向后移）

在这里插入图片描述

总结后的代码如下：

在这里插入图片描述

💻代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <vector>
#include <iostream>
using namespace std;

class Solution 
{
public:
    void moveZeroes(vector<int>& nums)
    {
        for (int cur = 0, dest = -1; cur < nums.size(); ++cur)
        {
            if (nums[cur])
            {
                swap(nums[++dest], nums[cur]);
            }
        }
    }
};

复写零

✏️题目描述：

在这里插入图片描述

✏️示例：

在这里插入图片描述

传送门：复写零

题解:

双指针问题在解题通常要求就地操作，但往往很难立马想出来，所以可以先进行异地操作拓展思路。本题的异地操作就是额外创建一个数组，然后据题意操作即可，很简单就不过多讲解

💻第一步： 先找到最后一个复写的数

从前往后复写会发现会出现前一个数把后一个数覆盖的情况，所以我们尝试从后往前复写，发现是可行的，所以唯一的要点就是找到那个开始复写的数

请添加图片描述

如图为示例 1 找到最后一个复写的数，那么是如何找到的呢？没有过多的技巧，就是要通过不断地画图尝试找到规律

• cur 表示最后一个复写的数
• dest 表示是否为最后一个数

在这里插入图片描述

如果 cur 的值为 0 ，dest 向后两位；如果 cur 的值为非 0 ，dest 向后一位。那么就延伸出另一个问题，要是 dest 越界了怎么办？

💻第二步： 处理越界情况并从后往前复写

如果越界了，那么 dest 所在的位置一般默认为 0 ，但是在平台上越界就会报错，且这种情况的时候一定是因为 cur 最后一个复写数为 0 导致的

请添加图片描述

所以我们只需将 n-1 处赋为 0，dest -= 2，cur-- 即可回到最后一个复写数为非0的情况

在这里插入图片描述

接着再完成从后向前复写的操作即可

💻代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <vector>
using namespace std;

class Solution 
{
public:
    void duplicateZeros(vector<int>& arr)
    {
        //1.先找到最后一个数
        int cur = 0, dest = -1, n = arr.size();
        while (cur < n)
        {
            if (arr[cur])
            {
                dest++;
            }
            else
            {
                dest += 2;
            }

            if (dest >= n - 1)
            {
                break;
            }

            cur++;
        }
        //2.处理边界情况
        if (dest == n)
        {
            arr[n - 1] = 0;
            dest -= 2;
            cur--;
        }
        //3.从后向前完成复写操作
        while (cur >= 0)
        {
            if (arr[cur])
            {
                arr[dest--] = arr[cur--];
            }
            else
            {
                arr[dest--] = 0;
                arr[dest--] = 0;
                cur--;
            }
        }
    }
};

快乐数

✏️题目描述：

在这里插入图片描述

✏️示例：

在这里插入图片描述

传送门：快乐数

题解:
💻解读题意：

据题意快乐数的判断分为两种情况

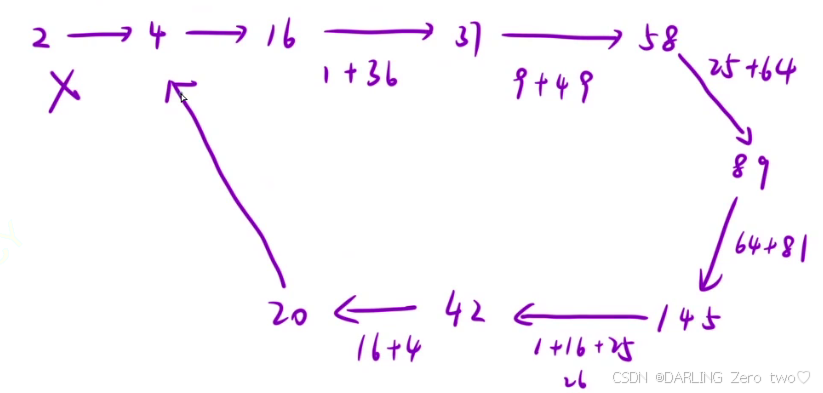
是快乐数 ，以 1 循环（以示例 1 为例）

在这里插入图片描述

不是快乐数，自循环（以示例 2 为例）

在这里插入图片描述

看到这里显然需要我们判断是否成环，在链表部分了解过，应该使用快慢指针

在这里插入图片描述

💻细节问题：

如果题目没有说明只有两种情况，那是不是可能会出现第三种情况：线性死循环
答案是不会的，以下是一些简单的证明，不影响本题，作了解即可

在这里插入图片描述

我们假设 n 可取的最大值为 9 × 10⁹ ，那么经过快乐数操作的数为 810，接下来无论进行多少次操作都是在[1，810]里的数，那么在经过大于 810 次操作后，根据鸽巢原理，必然会有重复，也就是成环，所以第三种情况不可能存在

💻代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
using namespace std;

class Solution
{
public:
    int bitSum(int n)
    {
        int sum = 0;
        while (n)
        {
            int t = n % 10;
            sum += t * t;
            n /= 10;
        }
        return sum;
    }
    bool isHappy(int n)
    {
        int slow = n, fast = bitSum(n);
        while (slow != fast)
        {
            slow = bitSum(slow);
            fast = bitSum(bitSum(fast));
        }
        return slow == 1;
    }
};

盛最多水的容器

✏️题目描述：

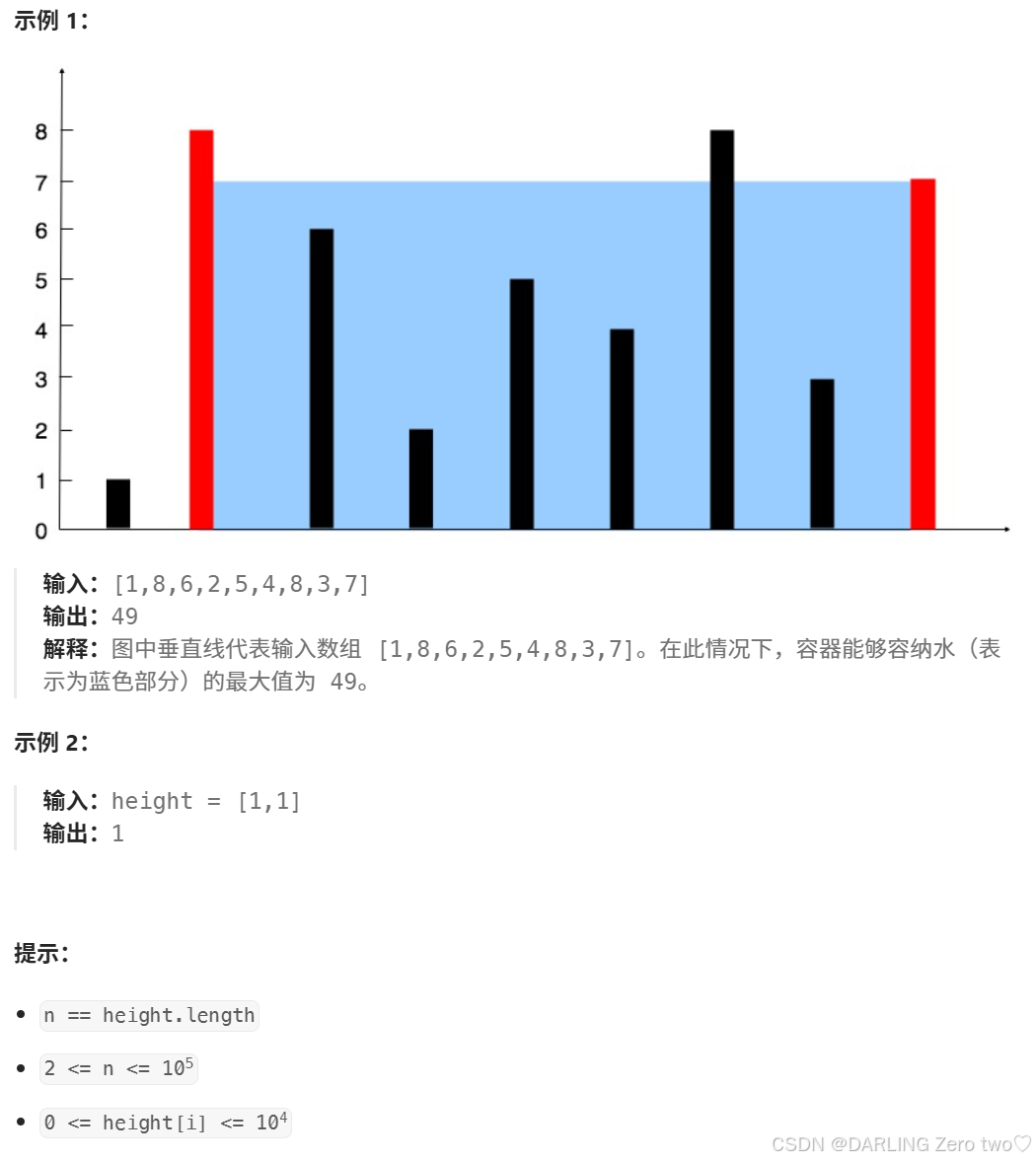
在这里插入图片描述

✏️示例：

在这里插入图片描述

传送门：盛最多水的容器

题解:

看到这道题一般最先想到的是用两层for循环暴力枚举，但在本题会超时，时间复杂度为 O(n²)，所以本题的思路是尽量把时间复杂度降为O(n)

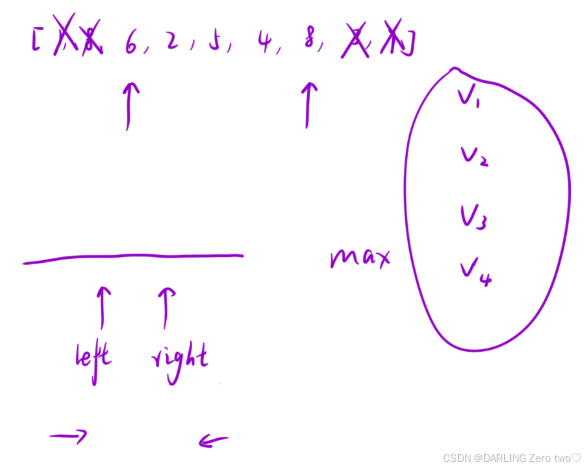
尝试减少枚举数量来降低时间复杂度，本题求的是体积，所以我们可以在标记开头和结尾的下标为 left 和 right

在这里插入图片描述

v 为体积，h 为高度，w 为宽度，可以发现在取两边的数计算宽度时，先固定一个不动，然后另一个逐渐缩小宽度，小的那个数缩小之后算出来的体积永远是小的，所以我们可以通过不断舍掉小的那个数缩小宽度，然后得出多个体积数，找出里面最大的那个

在这里插入图片描述

通过这种方式减少了不必要的枚举，降低了时间复杂度，只需遍历一遍数组就能得出最大的体积

💻代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <vector>
using namespace std;

class Solution 
{
public:
    int maxArea(vector<int>& height) 
    {
        int left = 0, right = height.size() - 1, ret = 0;
        while (left < right)
        {
            int v = (right - left) * min(height[left], height[right]);
            ret = max(v, ret);
            if (height[left] > height[right])
            {
                right--;
            }
            else
            {
                left++;
            }
        }
        return ret;
    }
};

希望读者们多多三连支持

小编会继续更新

你们的鼓励就是我前进的动力！

请添加图片描述