本章节是树结构的最后一篇——二叉树，这里我们只实现最简单的二叉树结构，在C++语法部分将学习更高阶的AVL树、红黑树巩固

二叉树的结构

1
2
3
4
5
6
7
8
typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：

  1. 空树
  2. 非空：根结点，根结点的左子树、根结点的右子树组成的

二叉树接口实现

二叉树节点创建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}
  1. 使用 malloc 函数为新节点分配内存，其大小为 BTNode 结构体的大小
  2. 检查内存分配是否成功。如果 malloc 返回 NULL，表示内存分配失败，使用 perror 函数输出错误信息，并返回 NULL
  3. 若内存分配成功，将传入的数据 x 赋值给新节点的 data 成员
  4. 将新节点的左右子指针 left 和 right 都初始化为 NULL，表示该节点暂时没有左右子节点
  5. 返回新创建的节点指针

二叉树树的创建

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
BTNode* CreatTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

由于现在对二叉树结构掌握还不够深入，为了降低学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式

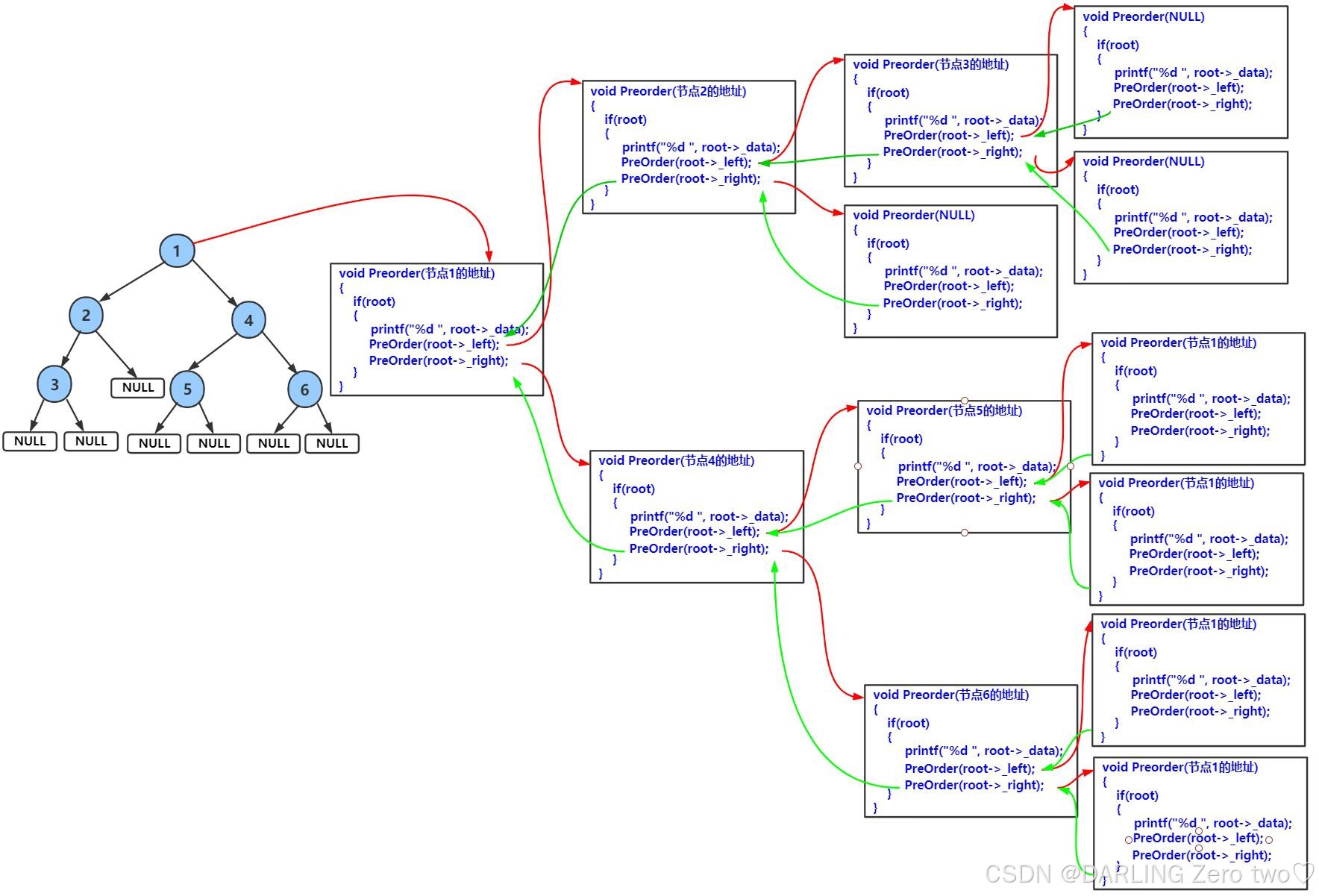
请添加图片描述

二叉树的前序遍历

1
2
3
4
5
6
7
8
9
10
11
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

前序遍历依据根、左子树、右子树的顺序，前序遍历又叫做深度优先遍历（DFS）

请添加图片描述

其本质上是一个有限递归的过程，当左节点递归到最后一个叶节点时，其子节点为 NULL ，向下递归就结束，然后开始回退遍历右节点

🔥值得注意的是： root == NULL 的 if 条件句既是为了表示空树的情况，也是为了结束向下递归的过程

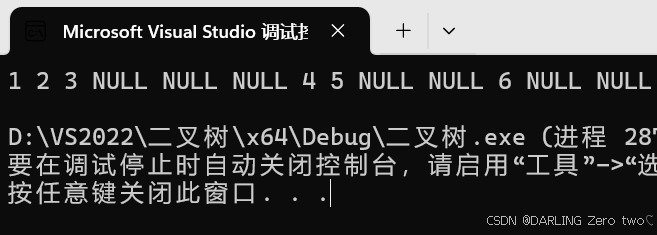
💻测试结果：

在这里插入图片描述

二叉树的中序遍历

1
2
3
4
5
6
7
8
9
10
11
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

中序遍历依据左子树、根、右子树的顺序

其余操作和前序遍历一致

💻测试结果：

在这里插入图片描述

二叉树的后序遍历

1
2
3
4
5
6
7
8
9
10
11
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

后序遍历依据左子树、右子树、根的顺序

其余操作和前序遍历一致

💻测试结果：

在这里插入图片描述

二叉树结点个数

1
2
3
4
5
6
7
8
9
10
void TreeSize(BTNode* root, int* psize)
{
	if (root == NULL)
	{
		return;
	}
	++(*psize);
	TreeSize(root->left, psize);
	TreeSize(root->right, psize);
}

获取节点个数首先想到的肯定是遍历二叉树，如上代码所示的方法，用一个移动指针遍历，每到一个节点就 ++ ，这固然可行，但是有更直观简洁的方法

⌨️优化代码：

1
2
3
4
5
6
7
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 :
		TreeSize(root->left)
		+ TreeSize(root->right)
		+ 1;
}

这种模式就像学校里的人数统计一样，假设想要统计全校寝室人数

  1. 寝室长统计寝室人数，汇报给宿管阿姨
  2. 宿管阿姨统计每栋宿舍人数，汇报给专业年级主任
  3. 专业年级主任统计专业人数，汇报给校长
  4. 最后由校长汇总专业年级主任上交的数据，就能得出全校寝室人数

这是一种清晰的统计流程，二叉树结点个数就是从最底下逐渐往上加和进行统计

二叉树高度获取

1
2
3
4
5
6
7
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	return TreeHeight(root->left) > TreeHeight(root->right)
		? TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
}

二叉树高度获取的思想和二叉树结点个数是一致的，高度取决于左子树和右子树路径较长的那条，直接比较然后递归取值即可

但是这段代码有个问题，比较时需要递归一次，比较完并没有保存每个节点高度的结果，获取结果的时候又要再递归一次，导致代码效率减慢

⌨️优化代码：

1
2
3
4
5
6
7
8
9
10
11
12
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight 
		? leftHeight + 1 
		: rightHeight + 1; 
}

所以每次向上回退时，保存每个节点的高度结果即可

二叉树第k层节点个数

1
2
3
4
5
6
7
8
9
10
11
12
int TreeKLevel(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;

	int leftK = TreeKLevel(root->left, k - 1);
	int rightK = TreeKLevel(root->right, k - 1);

	return leftK + rightK;
}

还是利用递归的思想，假设要获取第三层的节点个数，那么需要向上递归两次到达根节点，所以是 k - 1 次

从下往上数层数

  • 根节点处于第 1 层，对于根节点的左子节点和右子节点，它们处于第 2 层，距离第 3 层还有 1 层，所以递归调用 TreeKLevel(root->left, 2) 和 TreeKLevel(root->right, 2)

  • 当递归到第 2 层的节点时，对于它们的子节点（即第 3 层的节点），再次递归调用时传入 k - 1 即 1，此时满足 k == 1 的条件，返回 1 表示找到了一个第 3 层的节点

  • 通过不断地递归调用并使用 k - 1 作为新的层数参数，最终可以准确计算出二叉树中第 k 层的节点总数

二叉树查找值为x的节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;

	BTNode* lret = TreeFind(root->left, x);
	if (lret)
		return lret;

	BTNode* rret = TreeFind(root->right, x);
	if (rret)
		return rret;

	return NULL;
}
  • 递归查找左子树：
    如果上述两个 if 条件都不满足，说明当前节点不是目标节点，需要继续在其左子树中查找。递归调用 TreeFind(root->left, x) 来查找左子树中是否存在值为 x 的节点，并将返回结果存储在 lret 中。如果 lret 不为 NULL，说明在左子树中找到了目标节点，直接返回 lret
  • 递归查找右子树
    如果在左子树中未找到目标节点（即 lret 为 NULL），则继续在右子树中查找。递归调用 TreeFind(root->right, x) 来查找右子树中是否存在值为 x 的节点，并将返回结果存储在 rret 中。如果 rret 不为 NULL，说明在右子树中找到了目标节点，直接返回 rret
  • 未找到目标节点
    如果在左子树和右子树中都未找到值为 x 的节点，说明整个二叉树中不存在该节点，函数最终返回 NULL

二叉树的层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	while (QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);

		if (front->left)
			QueuePush(&q, front->left);

		if (front->right)
			QueuePush(&q, front->right);
	}

	QueueDestroy(&q);
}

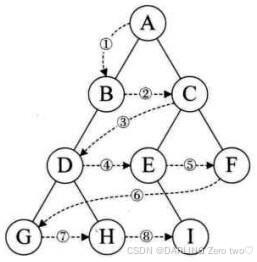
层序遍历就是从上到下，从左到右进行遍历，层序遍历也叫作广度优先遍历（BFS）

请添加图片描述

这里需要利用队列的特性来进行，出上一层，带入下一层（每出一个节点，就插入该节点的子节点）引入队列的头文件和源文件

传送门：【初阶数据结构】先来后到的秩序：栈和队列

🔥值得注意的是： BTNode* front = QueueFront(&q) 保存了二叉树的节点作为队列的头节点，释放时并不会影响到二叉树本身，而是释放队列头节点

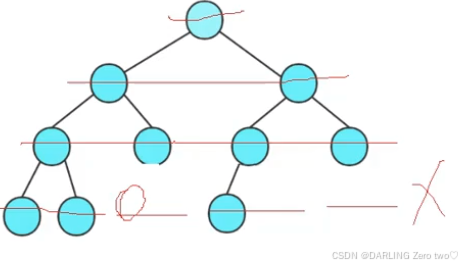
在这里插入图片描述

判断是否为完全二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
bool TreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	while (QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front == NULL)
			break;
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}

	while (QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

我们要知道一个特性：完全二叉树的非空节点一定是连续的

在这里插入图片描述

第一个循环是层序遍历二叉树，直到遇到第一个空就停下来，第二个循环是检查队列中剩余的节点是否都为空，继续遍历队列中剩余的节点，如果遇到非空节点，说明该二叉树不是完全二叉树，返回 false；如果队列中剩余的节点都为空，说明该二叉树是完全二叉树，返回 true

二叉树的销毁

1
2
3
4
5
6
7
8
9
10
void TreeDestroy(BTNode* root)
{
	if (root == NULL)
		return;

	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
	root == NULL;
}

希望读者们多多三连支持

小编会继续更新

你们的鼓励就是我前进的动力！

请添加图片描述